オイラーの公式をもっと味わう
フーリエ係数を求められることもわかり、これでめでたしめでたし…と言いたい所ですが、この後の話を進めるためにもう一工夫したいと思います。ここまで学んできたフーリエ級数はsinとcosという2種類の関数を組み合わせていました。フーリエ級数という考え方を理解するためにはこの書き方は直観的でわかりやすいのですが、実用的に使おうと思うと、sinとcosの計算をそれぞれ行う必要があって面倒です。もっとコンパクトに表現する方法はないものでしょうか。
結論から言うと、「オイラーの公式」をうまく当てはめてあげることで、sinとcosを1つの複素指数関数に統合することができます。これを「複素フーリエ級数」といいます。この時、フーリエ係数もまた複素数になり、「複素フーリエ係数」といいます。
…と、複素フーリエ級数の話をする前に、オイラーの公式は本当に重要&有用なものなので、しつこいようですがもう少しその意味を掘り下げておきたいと思います。話が脱線しているように見えるかもしれませんが、オイラーの公式と複素数についてしっかりイメージを固めておくことがこの後の話で大切になってきます。
オイラーの公式は、複素平面上の単位円上の点を表す
オイラーの公式
の右辺を見るとcosθとsinθは実数であり、a+ibという複素数の形そのものです。そして、「拡張された三角関数」を思い出してみると、sinθは偏角がθで単位円上にある点のy座標、cosθは偏角がθで単位円上にある点のx座標として定義されていました。つまりこの右辺は偏角θで「複素平面上の」単位円上にある点を表しています。
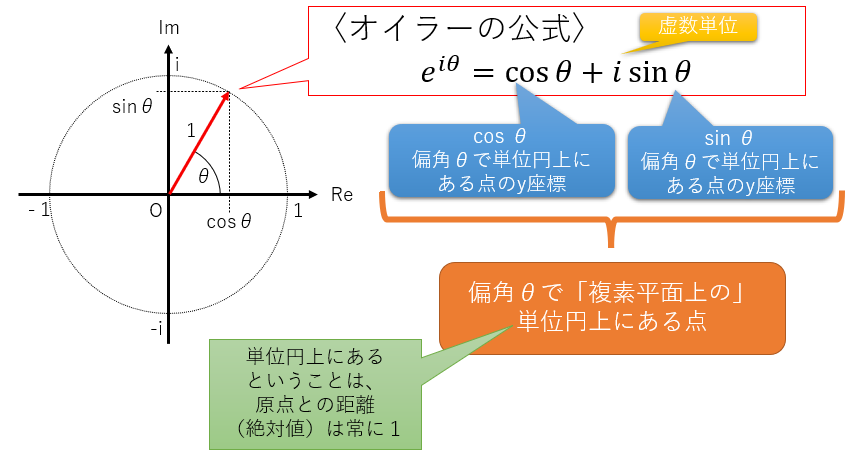

図1:オイラーの公式は、複素平面上の単位円上の点
複素数の極座標表示
複素数は実部と虚部を用いた直交表示(a+ib)の他に、偏角と絶対値を用いた極座標表示があるという事はすでにこの連載でお話ししました。
先の話から、オイラーの公式
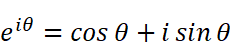
は偏角がθで絶対値が1の複素数を表していることになります。
この式に実数Aをかけ算すると、複素平面上の円の半径がA倍になります。すなわち、オイラーの公式に実数Aをかけ算すると偏角がθで絶対値がAである複素数を表すことができます。そのため
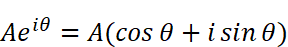
を指して「複素数の極座標表示」などと呼ぶことがあります。
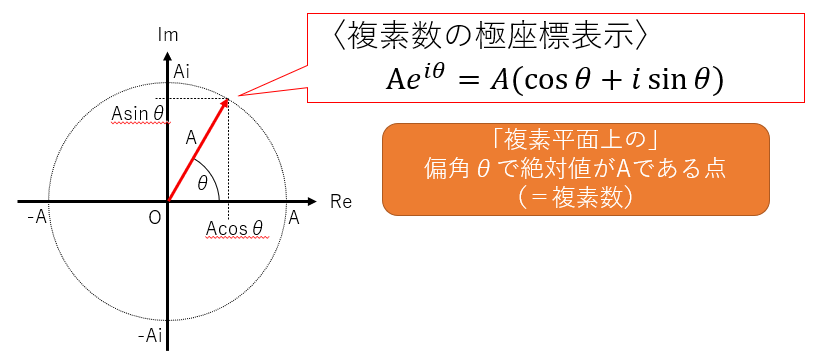

図2:複素数の極座標表示
複素数のかけ算とは、複素平面を「伸ばして」「回す」ことである
複素数の極座標表示を知ると、複素数同士の「かけ算」の性質が見えてきます。
2つの複素数

を考え、この2つをかけ算した結果を求めてみましょう。等号の左側が直交表示、右側が極座標表示です。
直交表示の複素数を使ってかけ算をすると
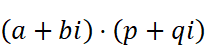
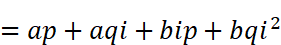
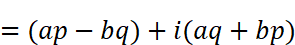
となります。間違ってはいないのですが、あまりきれいな式には見えません。
では今度は、極座標表示の複素数でかけ算をしてみましょう。途中の整理で指数法則を使用している事に注意して下さい。
ちょっと余談:指数法則
a,bが共に0でない時に成り立つ以下の関係式を、指数法則と言います。
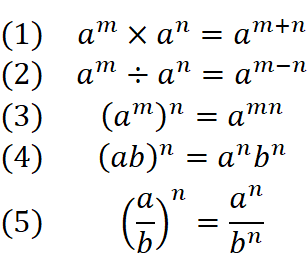
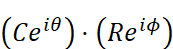
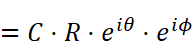
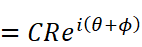
最終的に得られた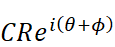
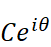
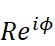
具体例を1つ挙げて、確認してみましょう。
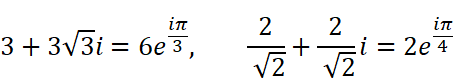
をかけ算してみます。極座標表示で計算すると
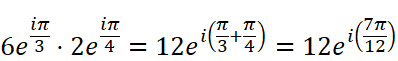
となります。
直交表示で計算してみると
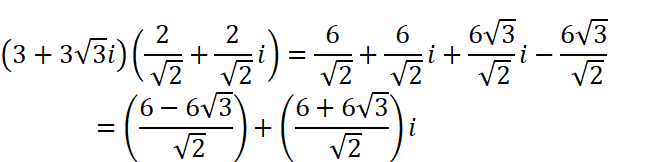
となります。ごちゃごちゃに見えますが、結果としては一致しています。
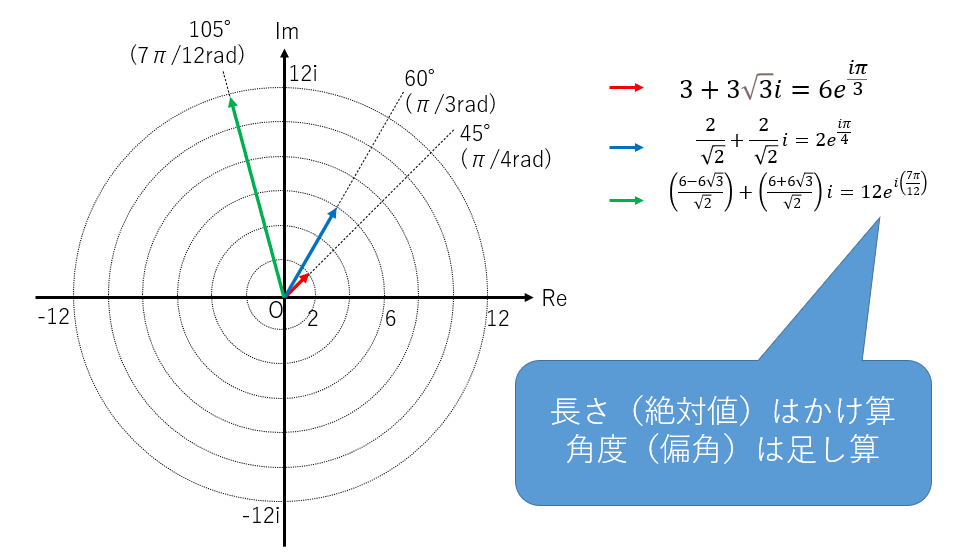

図3:複素数のかけ算
ちょっと余談:ド・モアブルの定理
高校数学で学ぶ複素数に関する定理で重要なものに「ド・モアブルの定理」があります。nを整数としたときに
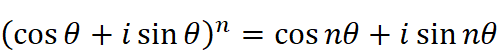
が成り立つというものです。
オイラーの公式を当てはめてあげると
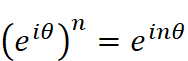
となり、実は単純な指数法則であることがわかります。
あるいはこれを複素数の極座標表示とみなせば、絶対値が1で偏角がθである複素数をn回かける計算なので、絶対値は1だから何回かけても1のままで、偏角だけがかけ算をするたびにθ回転して、最終的にnθになる、ということがイメージできると思います。
オイラーの力でAkとBkを統合する
冒頭の繰り返しになりますが、オイラーの公式を使うと、sinとcosが併用されていたフーリエ級数展開をぐっとコンパクトにすることができます。これを「複素フーリエ級数」といいます。この時、フーリエ係数もまた複素数になり、「複素フーリエ係数」といいます。
結論としてどのような式になるかと言うと、次のような式になります(どうしてこのような式になるか気になる人は、末尾の付録をチェックして下さい)。
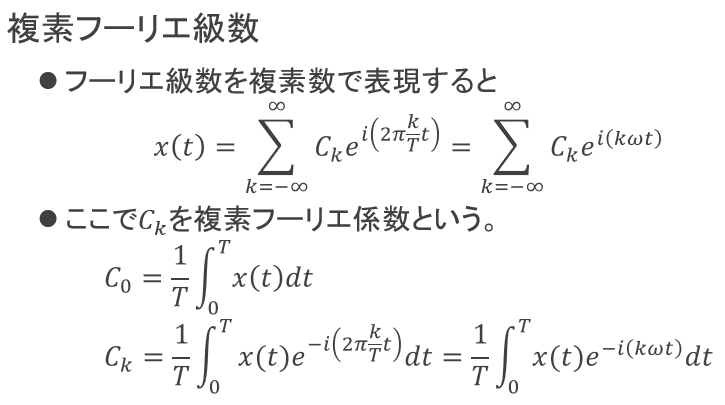
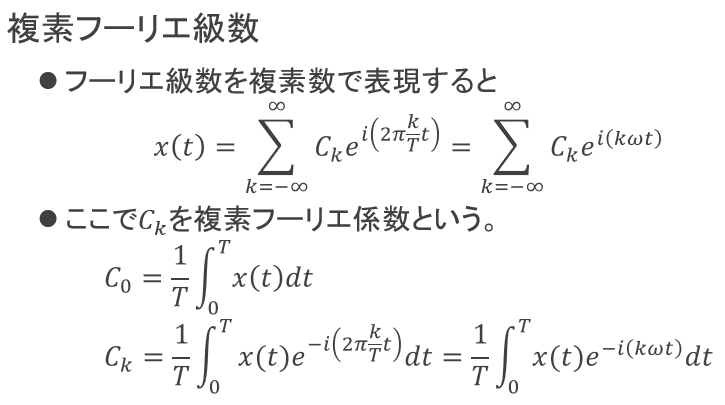
図4:複素フーリエ級数
複素フーリエ級数は、複素フーリエ係数Ck(名前の通り、これは複素数です)と、複素平面上の単位円上にある点をかけ算しています。これは時刻tが進むにつれてkωの速度で各成分を回転させながら、全ての成分を足し合わせると元の関数x(t)が再現されると主張しています。(難しいな、と思う人はとりあえず眺めておくだけでもOKです!)
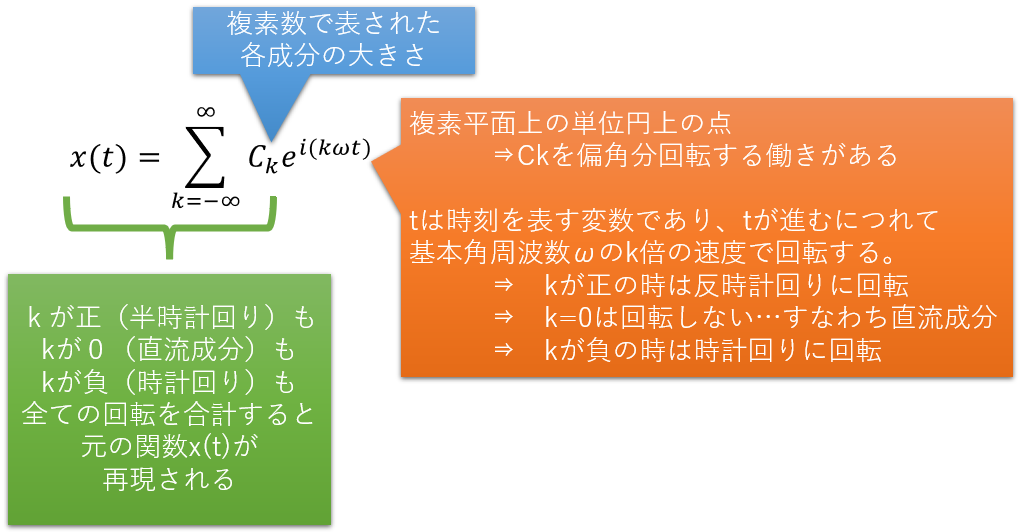

図5:複素フーリエ級数を読み解く
次回はフーリエ級数を発展させて「フーリエ変換」の世界に進みます!
付録:複素フーリエ級数の公式を導出する
フーリエ級数展開の公式に、オイラーの公式から導出した複素形式の三角関数を当てはめます。
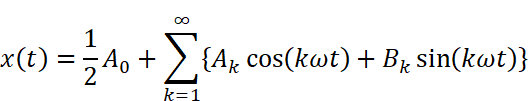
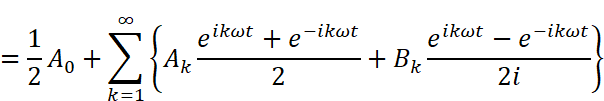
分数をばらした後、分母に虚数単位がある所は 
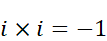
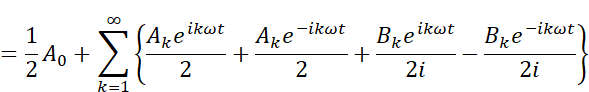
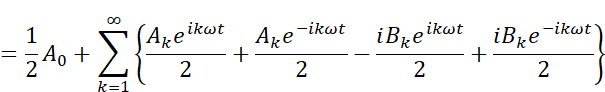
分母が全て2に揃ったので、指数関数の指数が正の項と負の項でまとめて整理してあげます。
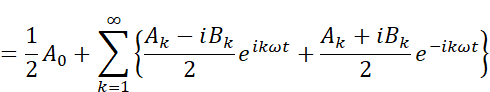
今、総和記号のループ変数kは1から無限大の範囲ですが、これを-∞から∞の範囲にすると、指数関数の指数が正の項と負の項を1つにまとめることができます。(k=0は周波数が0、すなわち直流成分を表すこととします)。AkとBkは実数であり、正でも負でも自由に定義できますから、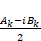
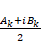
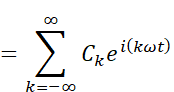
と整理することができます。(kωtのカッコは本質的には不要ですが、分かりやすくするために追加しました)
こちらも是非
“もっと見る” ブログ
はじめての耐量子暗号
量子コンピューティングはさまざまな面で明るい未来のために期待される技術である反面、その演算能力をセキュリティ上の攻撃に使われることを考えると、既存の暗号技術にとって深刻な脅威でもあります。
Arm®対応のWindows IoT OS 【Windows IoT on Arm】を評価ボードで動かしてみる
組み込み機器向けOS、Windows 10/11 IoT Enterprise(以下Windows IoT)がサポートするArmプラットフォームが拡大しています。Windows IoT on Armは、Windows IoTのメリットそのまま、より低コストで低消費電力というArmならではのメリットもございます
センサーのすべてがわかる!組み込み技術者のための基礎知識
私たちの生活を豊かにするために欠かせないセンサー。そんなセンサーの仕組みや種類について、分かりやすく解説していきます。














