フーリエ級数の大きな制約
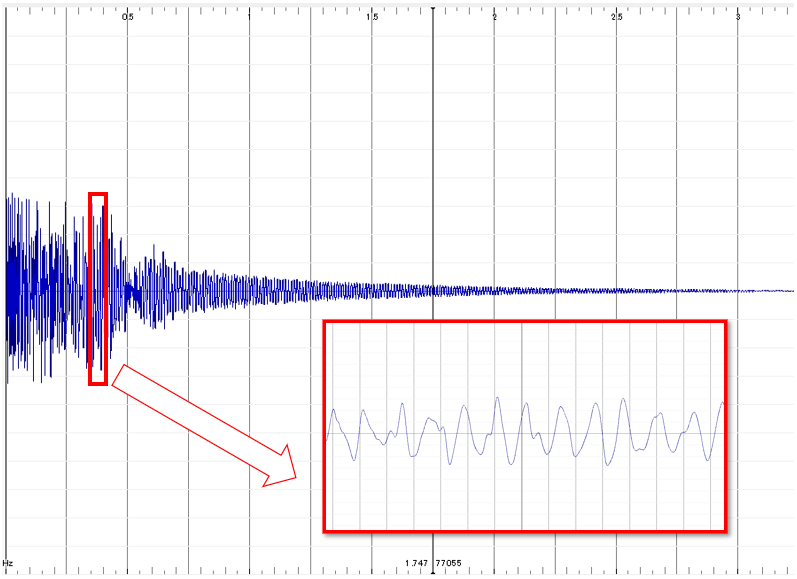
図1：和太鼓の音波
図1に示した波形は、和太鼓を一発だけドンッと叩いた音です。（ 効果音ラボ様配布の「和太鼓でドン.mp3」をSonic Visualiserで可視化しました。）
これも音（＝空気の「振動」）なので、大きく拡大したミクロな視点で見れば、部分部分はある程度周期的な波形になっています。しかし縮小してドンッ全体の波形をマクロな視点で見れば、最初の〈ド〉ンッの部分だけ波形が大きく、ド〈ンッ〉の部分は尻つぼみになっています。太鼓は一発しか叩いていませんので、この先ずっと録音を続けても、波形は尻つぼみのままどんどん小さくなって、最終的には0（振動無し）になります。
つまりこの太鼓の音波形は、マクロな視点で見れば「繰り返さない波形」であり、「単発波形」と呼ばれます。しかしここまで学んできたフーリエ級数展開は、「入力信号が周期波形でなければならない」という制約がありました。上図のような太鼓の音、すなわち単発波形は、フーリエ級数展開できないのでしょうか。
フーリエ級数展開からフーリエ変換へ
単発波形を何とかしてフーリエ級数展開するには
どうやったら、「単発波形をフーリエ級数展開」できるのかを考えたいわけですが、このままでは先に進めません。そこで発想を転換します。
周期波形であればフーリエ級数展開できて、単発波形ではフーリエ級数展開できないわけですから、「単発波形を（無理やり）周期波形に変換」できれば、フーリエ級数展開で扱えるようになるはずです。これを図解すると図2のようになります。図では単発波形として先ほどの太鼓の波形を簡略化したイメージで直角三角形型に描いています
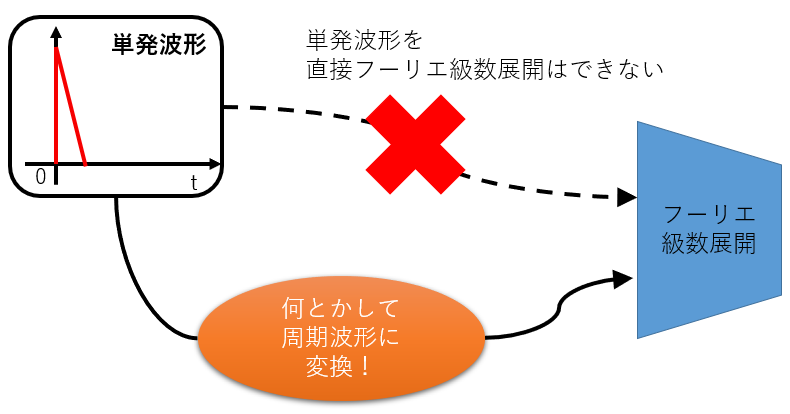
図2：単発波形をどうやって分析するか
図3①の単発波形を（むりやり）周期波形にするため、同じ直角三角形を隙間なく並べた波形、図3②を考えます。するとこれはもはや、以前計算した「ノコギリ波」の一種であって、フーリエ級数展開できることは明らかです。
次に、図3②を1つおきに「間引き」した波形、図3③を考えます。山と山の間に隙間ができて（＝周期が2倍になって）ノコギリ波ではなくなりましたが、これもまた同じ形〈山＋休み〉が繰り返される周期波形とみなせるので、フーリエ級数展開可能です。
同様に図3③を1つおきに「間引き」した波形、図3④も、山と山の間にできた隙間が広がった（＝周期が4倍になった）ものの、明らかに〈山＋休み＋休み＋休み〉が繰り返される周期波形ですから、フーリエ級数展開が可能です。
このように「間引き」を繰り返していくたびに、山と山の間にできた隙間は広がって（周期が間引きの度に2倍されて）いきますが、「周期波形である」ことに変わりはありません。この手続きを極限まで繰り返せば、つまり1つ目の山と2つ目の山の間に無限時間の隙間ができて、周期が無限大になるまで間引きをしたら…それでもやはり「周期波形である」とみなせると考えます。
まるで狐につままれたように思えるかもしれませんが、このように考えることで、実は「単発波形は、周期無限大の周期波形である」ととらえることができるのです。
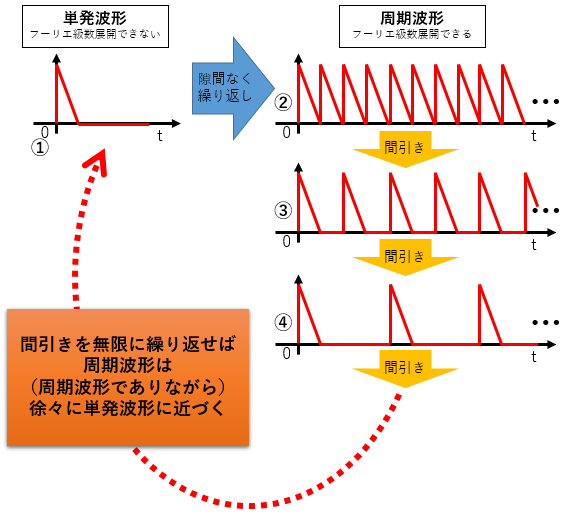
図3：周期波形を間引きながら単発波形に近づける
単発波形の周波数成分はどうなるのか
今度は図3の流れで「単発波形を（無理やり）周期波形に変換」した後、「間引き」を行った結果周波数成分がどのように変化していくかを詳しく考えてみましょう。
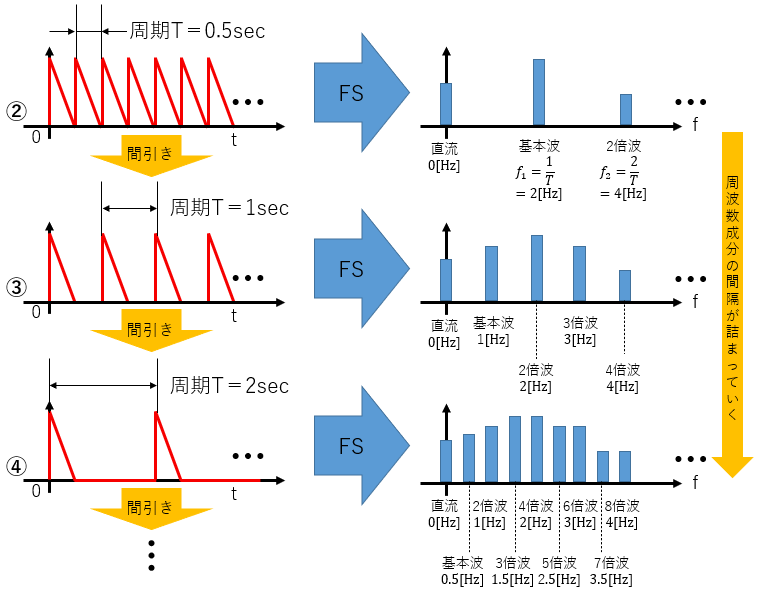
図4：間引きとスペクトルの関係性
元の単発波形である直角三角形の横幅（＝時間）が、0.5[sec]だとしましょう。すると、この三角形を隙間なく並べて周期波形にした図4②（図4の②～④は図3の②～④と対応しています）では、波形の周期Tは0.5[sec]ということになります。これをフーリエ級数展開（FS）により周波数領域に変換すると、直流成分（0[Hz]）、基本波（1/0.5＝2[Hz]）、2倍波（2/0.5＝4[Hz]）、3倍波（3/0.5＝6[Hz]）…という、2[Hz]間隔の成分に分離されることになります。
これを1つおきに間引きした図4③では、波形の周期Tは2倍となって1[sec]となります。これをフーリエ級数展開（FS）により周波数領域に変換すると、直流成分（0[Hz]）、基本波（1/1＝1[Hz]）、2倍波（2/1＝2[Hz]）、3倍波（3/1＝3[Hz]）…という1[Hz]間隔の成分に分離されます。
同様にさらなる間引きをした図4④では、波形の周期Tはさらに2倍の2[sec]です。これをフーリエ級数展開（FS）により周波数領域に変換すると、直流成分（0[Hz]）、基本波（1/2＝0.5[Hz]）、2倍波（2/2＝1[Hz]）、3倍波（3/2＝1.5[Hz]）…という0.5[Hz]間隔の成分に分離されます。
つまり間引きによって元波形の周期が2倍、4倍、8倍…と倍々になっていくにつれて、周波数成分の間隔は1/2、1/4、1/8…と半分になっていき、ぎゅっぎゅっと「詰まっていく」ことになります。
基本波、2倍波、3倍波…という飛び飛びの成分を持つスペクトル（周波数成分）を「離散スペクトル」といいます。間引きを重ねて周期を伸ばしていく事で離散スペクトルの間隔がぎゅっぎゅっと詰まっていくと、究極的には（周期が∞≒単発波形になった）スペクトルのすき間は見えなくなります。このようなスペクトルを「連続スペクトル」といいます（図5）。
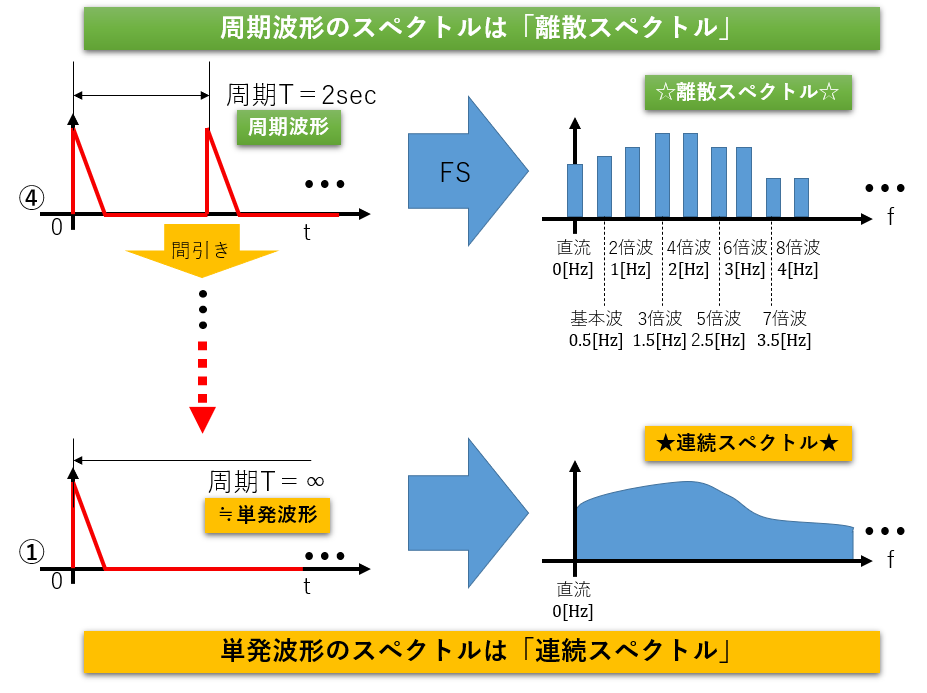
図5：単発波形のスペクトルは連続スペクトル
単発波形の分析を実現するフーリエ変換
以上の考え方を使ってフーリエ級数展開を発展させて、単発波形の分析を実現したものが「フーリエ変換」です。
できるだけ具体的なイメージを掴んでもらうために長々と説明してきましたが、フーリエ変換の公式そのものは、すでに紹介した「複素フーリエ係数Ckを求める公式」を自然に発展させたものと考える事ができます。両者の比較を図⑥に示します。
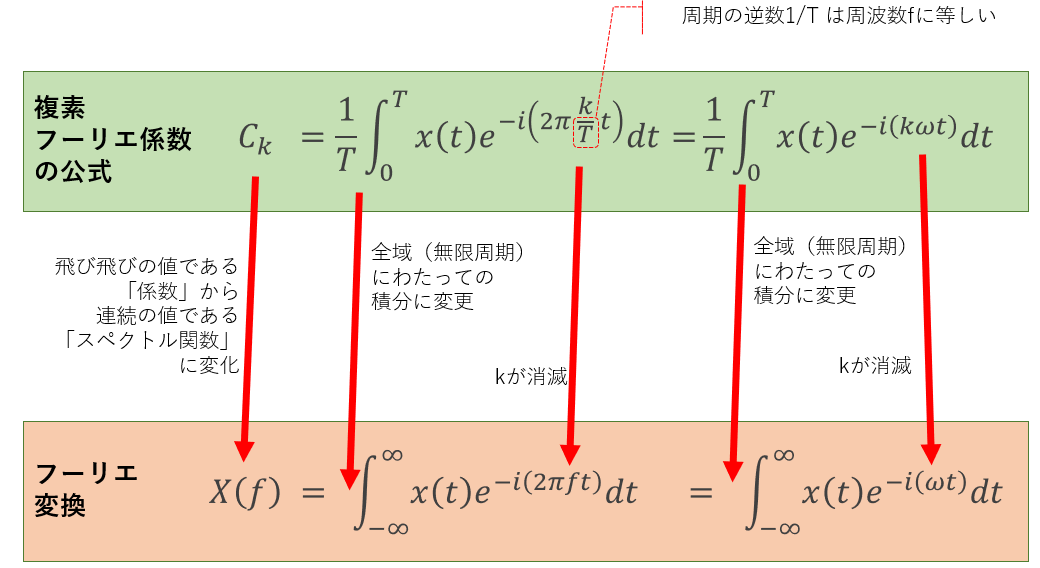
図6：複素フーリエ係数の式からフーリエ変換へ
複素フーリエ係数が複素数であったように、スペクトル関数X(f)の出力も複素数です。「振幅スペクトル」「位相スペクトル」「パワー（エネルギー）スペクトル」の求め方は、複素フーリエ係数と同様です（図7）。
図7：フーリエ変換からスペクトルを求める
ちょっと余談：なぜ「係数」の公式から「フーリエ変換」が得られるのか
「フーリエ級数」を進化させたものが「フーリエ変換」だと言いながら、その公式は「フーリエ係数」の公式から導かれていることを不思議に思う（または気持ち悪く思う）人がいるかもしれません。
これは歴史的な都合なので致し方ないのですが、元々の「フーリエ級数」は「複数の正弦波の合成で任意の周期関数を得られる」という、「周波数領域⇒時間領域」の関係性に着目したものでした。
一方「フーリエ変換」は「非周期関数を周波数成分に分解する」という「時間領域⇒周波数領域」の関係性に着目したものであり、フーリエ級数とフーリエ変換では、時間領域と周波数領域のどちらを基準に捉えるかが異なっているのです。
フーリエ級数とフーリエ変換の対比関係を図に整理すると図8のようになります。
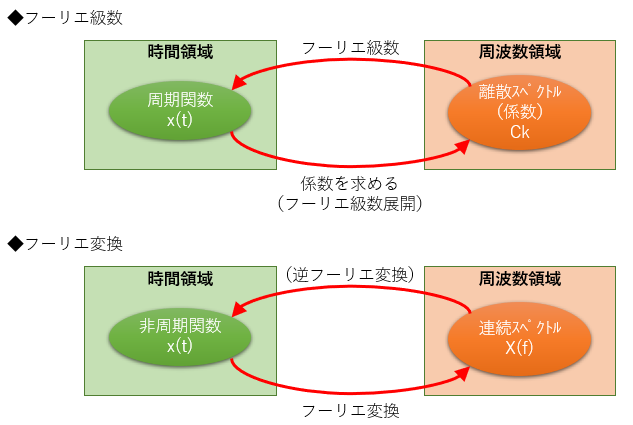
図8：フーリエ級数とフーリエ変換の対比
次回はフーリエ変換の具体例として、矩形単発パルスをフーリエ変換してみます。
こちらも是非
“もっと見る” ブログ
センサーのすべてがわかる！組み込み技術者のための基礎知識
私たちの生活を豊かにするために欠かせないセンサー。そんなセンサーの仕組みや種類について、分かりやすく解説していきます。
ブラシレスモーター制御用MCUをささっと動かしてみよう！【RL78編】
私の主観としては、”モーター制御用途でも十分使用可能な超汎用MCU”です。現状最も人に勧められるMCUの1つです。2つめのリンク stmcu.jpは、ログインする事でリファレンスマニュアルやペリフェラルの使い方に関する日本語資料が閲覧できますので、ユーザー登録をおススメします。
【フーリエ級数編3：フーリエ級数展開】イメージでしっかりつかむ信号処理〜基礎から学ぶFFT〜
いよいよ、フーリエさんの発見したフーリエ級数展開を学んでいきます。『全ての周期信号は三角関数（サイン波・コサイン波）の足し合わせで表現できる』と言葉ではすでに説明しましたが、これを数式を使って定義すると、図のようになります。