はじめての耐量子暗号

量子コンピューティングの脅威を整理する
耐量子暗号(PQC)のアルゴリズム
アルゴリズムの標準化
アルゴリズムの実際
PQCを動作させてみる
まとめ

量子コンピューティングの脅威を整理する

量子コンピューティングはさまざまな面で明るい未来のために期待される技術である反面、その演算能力をセキュリティ上の攻撃に使われることを考えると、既存の暗号技術にとって深刻な脅威でもあります。量子コンピューティングと一口に言っても、そのような暗号解読に利用できるためにはエラーのない演算処理が可能な、いわゆるFTQC: Fault-Tolerant Quantum Computingが必要です。しかし、それが実現すると量子コンピューティングが得意とする素因数分解や離散対数問題などは従来型コンピュータに比べて桁違いの速さで解けてしまうことが予測されています。

鍵サイズ	従来型コンピュータ	量子コンピュータ
RSA-768	2年（スーパーコンピュータ）	数秒
RSA-1024	数百年	数分〜1時間
RSA-2048	数千年以上	数時間以内

表1: 素因数分解、離散対数問題の処理速度予測

では、既存暗号技術の中でどのようなものが量子コンピューティングによって脅威となるのか、少し振り返ってみることにしましょう。

暗号といえば、最初に思い浮かべるのは、平文のメッセージを暗号鍵を使って他人に読めないように暗号化し、受信側も同じ鍵を使って復号する暗号技術かと思います。このような、暗号化と復号に同じ鍵を使って大量のメッセージを暗復号する技術を対称鍵暗号と呼びます。

暗号アルゴリズムのAESは非常に広く使われている暗号アルゴリズムなので、AESという言葉をどこかでお聞きになったことがあるかと思います。その暗号化の手順はかなり複雑ではありますが、暗復号に同じ鍵を使う対称鍵暗号の一つです。

対称鍵暗号は大量のメッセージを効率的に暗復号できるのですが、復号のための鍵を安全に通信相手に送らなければならないという重大な課題があります。そのために使われる方法の一つとしてディフィーヘルマンによる鍵共有という方法があります。この方法は、途中情報を攻撃者に知られても最終的な鍵は安全に相手と共有できる、公開鍵方式の一つです。

公開鍵の技術は、安全な署名と検証のためにも使われます。この場合、署名者は署名鍵が漏洩しないように管理していれば、署名検証のための検証鍵は公開鍵として相手に渡しても安全に正しく検証することができます。

現代のシステムでは、暗号技術は多岐にわたる用途で使われていますが、ここでは、ご覧のように大きく二つの利用シナリオを取りあげてみましょう。安全なネットワーク通信のためのプロトコルと、安全なブートロード、ファームウェア更新のための検証シナリオです。

安全なネットワーク通信では、次のようなセキュリティ要素を実現します。

通信相手の認証(正しい相手であることを確認)
メッセージの秘匿化(暗号化)
メッセージの一貫性、真正性(改ざん検出)

安全なブートロード、ファームウェア更新では、次のような要素を実現します。

メジャードブート、コードの署名検証
不正なファームウェア更新、ロールバック攻撃の検出

表2では、その二つの利用シナリオで使われている暗号技術をまとめてみました。それらの暗号技術は、大きくは公開鍵系のものと対称鍵系の二つにわかれます。

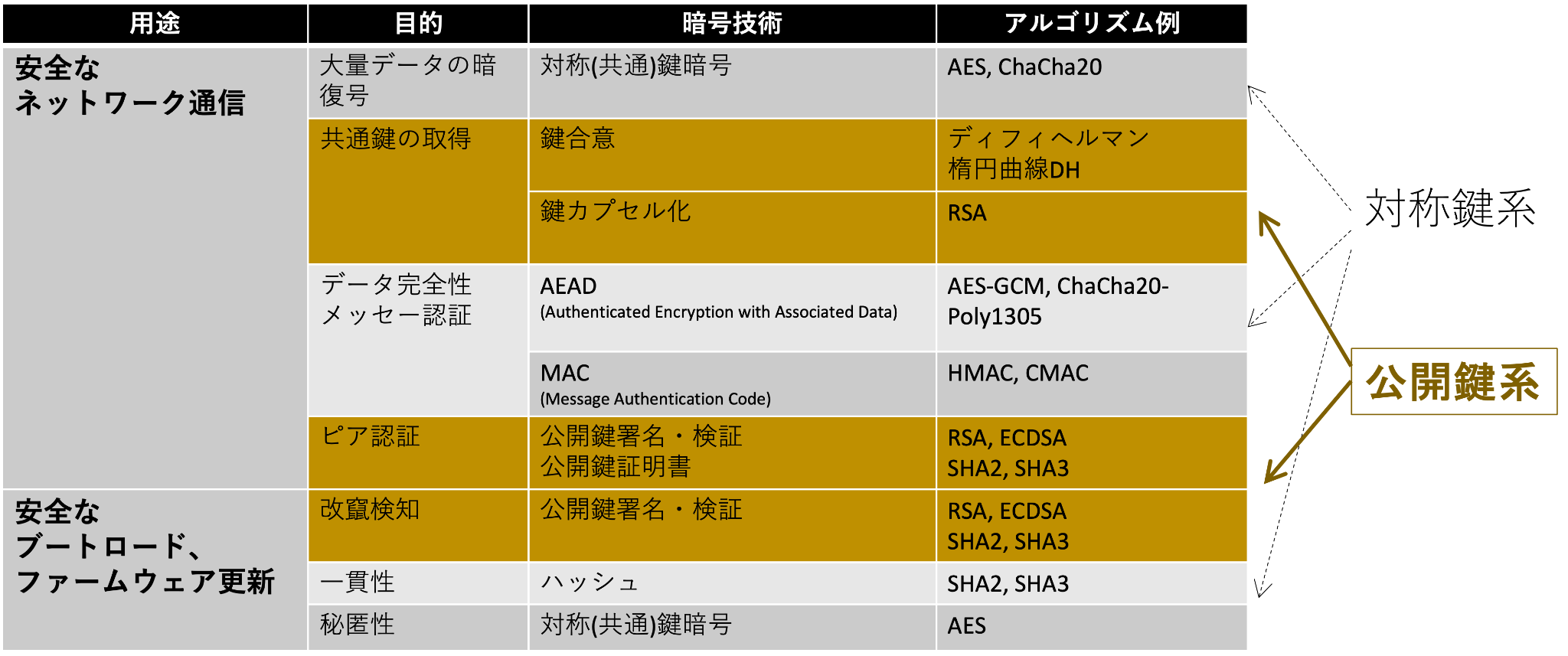
表2: 暗号技術の分類

この二つに分類したのは、量子コンピュータによる攻撃方法として、公開鍵系と対称鍵系とそれぞれの方法が知られているからです。対称鍵系への攻撃方法であるGroverのアルゴリズムでは計算量を平方根に削減することができることが知られていますが、これは従来アルゴリズムの変更なしに鍵長を２倍にすれば量子コンピュータによる攻撃に対しても従来技術の場合と同等の暗号強度を保つことができることを意味しています。

一方、公開鍵系へのShorのアルゴリズムは、従来技術では数百年、数千年かかる素因数分解、離散対数問題を数分、数時間と桁違いに高速に解くことができると言われています。それに対抗するためには単純に鍵長を長くしただけでは不十分であり、新しいアルゴリズム、新しいスキームを用意する必要があります。
それが耐量子暗号、Post Quantum Cryptography(PQC)です。

冒頭にも紹介したように、量子コンピューティングが暗号解読に使えるようになるのは少し先かも知れません。しかし、開発プロセス、製品ライフサイクルの長い製品、あるいは市場に一旦出回るとコードの更新が難しい製品組み込み型のもの、あるいは、情報、データのライフサイクルの長いものについては、攻撃対象のデータを今収集しておいて将来解読するという、いわゆるHarvest Now, Decrypt Later（HNDL）攻撃も知られています。そろそろ、この種の脅威について真剣に考えるべきタイミングとなっているように思われます。

耐量子暗号(PQC)のアルゴリズム

こうした認識に基づいて、米国連邦政府の暗号アルゴリズム利用のガイドラインであるCNSA( The Commercial National Security Algorithm)も2022年に改版され、そのCNSA2.0では、PQCへの対応について、2030年までの準備期間、2033年までの全面移行を推進していて、同じような動きは欧州、日本でもそれぞれの形で進められています。

図1: CNSA2.0のタイムライン

そんな中で、2017年には米国NISTによる公開鍵暗号とデジタル署名に関するアルゴリズムのコンペティションが開催され、2024年には第3ラウンドの結果を受けて、鍵カプセル化とデジタル署名についての標準が発行されています。また、つい先日になりますが、その後の第4ラウンドの結果も発表され、鍵カプセル化のアルゴリズムが追加されることになりました。

第1ラウンド（2017年12月～2019年1月）	69の候補アルゴリズム
第2ラウンド（2019年1月～2020年7月）	69 → 26
第3ラウンド（2020年7月～2022年7月）	26→最終候補7、代替候補8 選定（2022年7月）　鍵カプセル化　• CRYSTALS-Kyber（ML-KEM）　デジタル署名　• CRYSTALS-Dilithium（ML-DSA）　• FALCON（標準化作業中）　• SPHINCS+（SLH-DSA）
第4ラウンド	選定（2025年3月）鍵カプセル化 HQC (Hamming Quasi-Cyclic)

表3: NIST PQCコンペティションのまとめ

では、PQCのアルゴリズムとはどんなものか少し見てみることにします。まずは、公開鍵暗号が鍵を公開してもよい理由ですが、従来型暗号でもPQCでも一方向関数にあります。つまり、ある入力 x から出力 f(x)を計算することは簡単だけれど、その逆方向の演算は大変難しい、というような演算を使います。例えば、従来型暗号の公開鍵暗号として広く使われているRSAの場合では、大きな整数の積(p x q) を求めることはそれほど難しくないけれど、大きな整数の素因数分解は難しいという事実を使います。

前述のNISTが行ったPQCアルゴリズムのコンペティションでは、量子コンピュータによる攻撃に耐える何らかの一方向性関数を使ってKEM (Key Encapsulation Mechanism) が実現できることを目標の一つとしました。KEMでは次のように公開鍵と秘密鍵のペアを生成し、公開鍵を使って暗号化、秘密鍵を使って復号します。

鍵ペアの生成 (Key Generation)
公開鍵と秘密鍵の生成
カプセル化 (Encapsulation)
公開鍵を使った暗号化
復号 (Decapsulation)
秘密鍵を使った復号

これを、クライアントとサーバ間で安全な通信を行うために共通鍵を交換するというシナリオに当てはめると、図2のようになります。Client側がまず公開鍵と秘密鍵のペアを生成します。公開鍵はServer側で生成した共有値のカプセル化に使います。秘密鍵はClientが受け取ったカプセル化された情報を復元するために使用します。

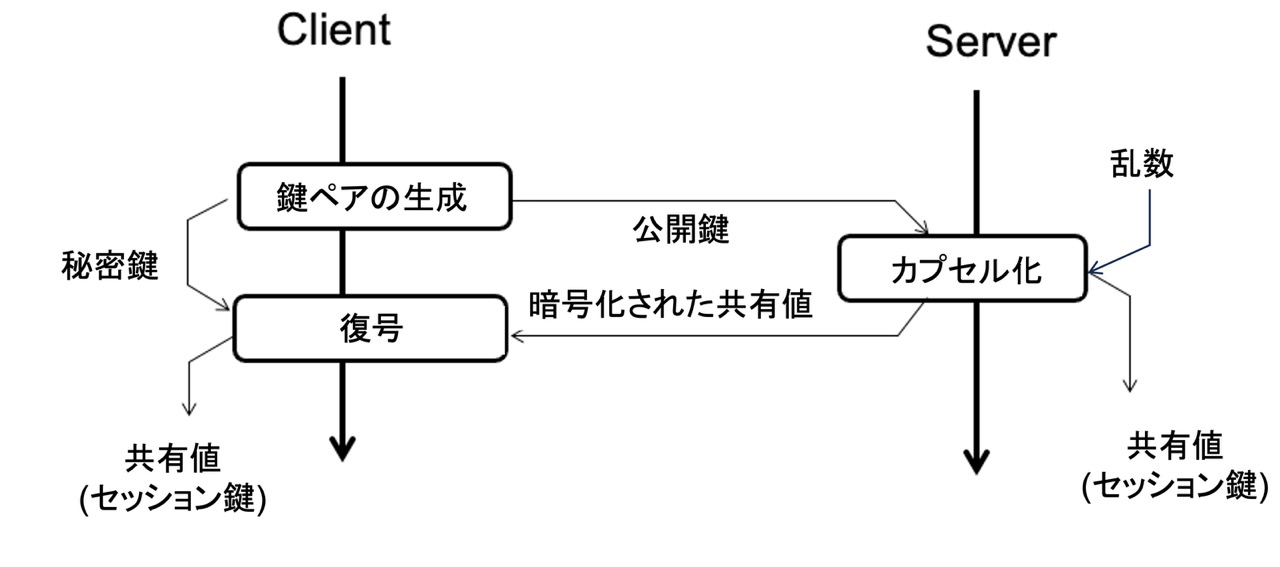
図2: KEMモデルによる鍵交換

NISTのコンペティションのもう一つのゴールは、署名検証のためのPQCアルゴリズムで、次のように、鍵ペアの生成、署名、検証の操作を実現します。アルゴリズムがPQCである点を除けば、使い方は従来型の公開鍵署名と同様です。

鍵ペアの生成 (Key Generation)
署名鍵と検証鍵の生成
署名 (Signature Generation)
署名鍵でメッセージの署名を生成
検証 (Signature Verification)
検証鍵でメッセージの署名を検証

ここで、具体的なPQCアルゴリズムについて説明します。NISTコンペティションでもさまざまなアルゴリズムが提案されましたが、その中で勝ち残ったのも含めて多くの候補がベースとしていたのはご覧の格子暗号と呼ばれるものです。

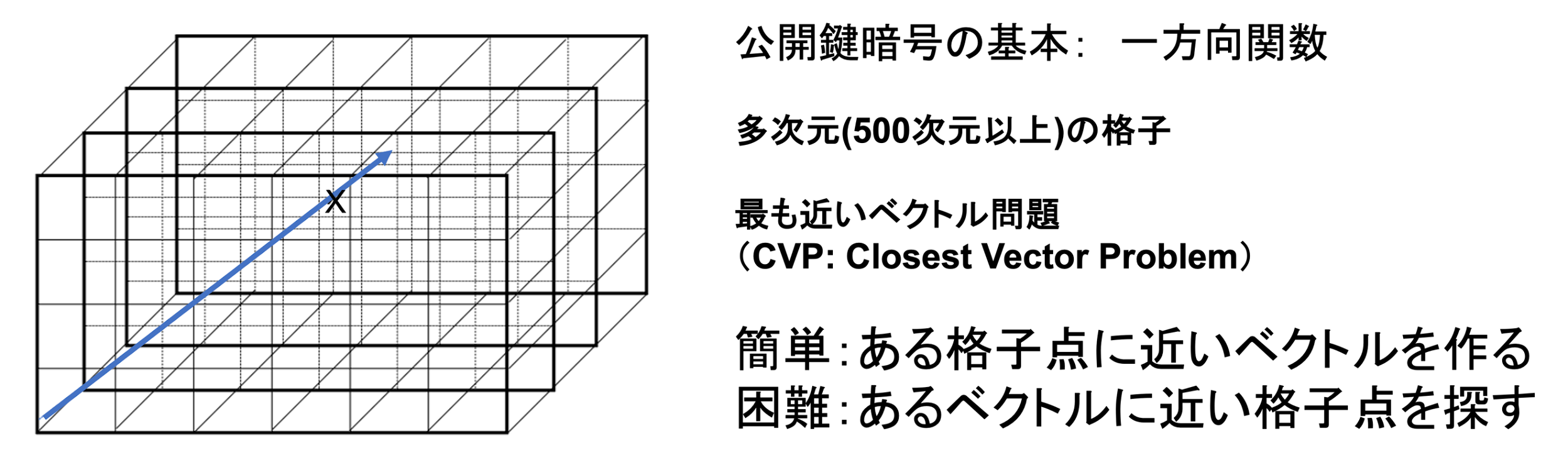
図3: 格子暗号

実際の格子暗号では、500, 1000次元といった多次元の格子を使いますが、この図では直感的にわかるように３次元にしています。格子暗号では、この多次元格子空間である格子点に近いベクトルを作るのは簡単だけれど、逆に与えられたベクトルに近い格子点を探すのは困難だという性質を使います。

ただし、それだけでは安全とはならないので、例えば、コンペティションの最終候補だったKyber、後に標準化されてML-KEMと呼ばれているアルゴリズムではさらに格子点にノイズを加えるLWE（誤り付き学習問題）が使われています。また、このような演算は直感的には浮動小数点演算になりそうですが、Ring-LWEという手法で整数演算化することでサイドチャネル攻撃のような攻撃にも対処しています。

NISTコンペティンションの第4ラウンドで勝ち残ったHQCでは格子暗号とは違った方法が使われています。こちらでは、誤り訂正符号に基づくもので、メッセージに所定の変換を加えると、その変換方法を知っていれば誤り訂正が可能だけれど、知らないと誤り訂正は困難となる、という性質を使っています。その変換方法というのが秘密鍵となります。この基本原理自身は以前から知られていたのですが、鍵や暗号化された暗号文の長さが非常に大きくなることが課題でした。HQCではこれをLWE (誤り付き学習問題) に近い方法を利用して、まだ多少大きいながらも鍵や暗号文を実用的なサイズに圧縮することに成功しています。

一方、先ほどの格子暗号やHQCのような鍵カプセル化には利用できないのですが、署名検証のためのアルゴリズムとして階層型ハッシュという方法が知られています。
階層型ハッシュでは、Merkleツリーと呼ばれるハッシュのツリー構造を利用します。図4の一番下のリーフノードのそれぞれに乱数値を割当て、隣り合ったリーフの乱数値を合わせたもののハッシュ値を取り親のノードの値とするというようにツリーを構成します。もちろん、実際には十分な数のリーフを持つ多段のツリーを使用します。

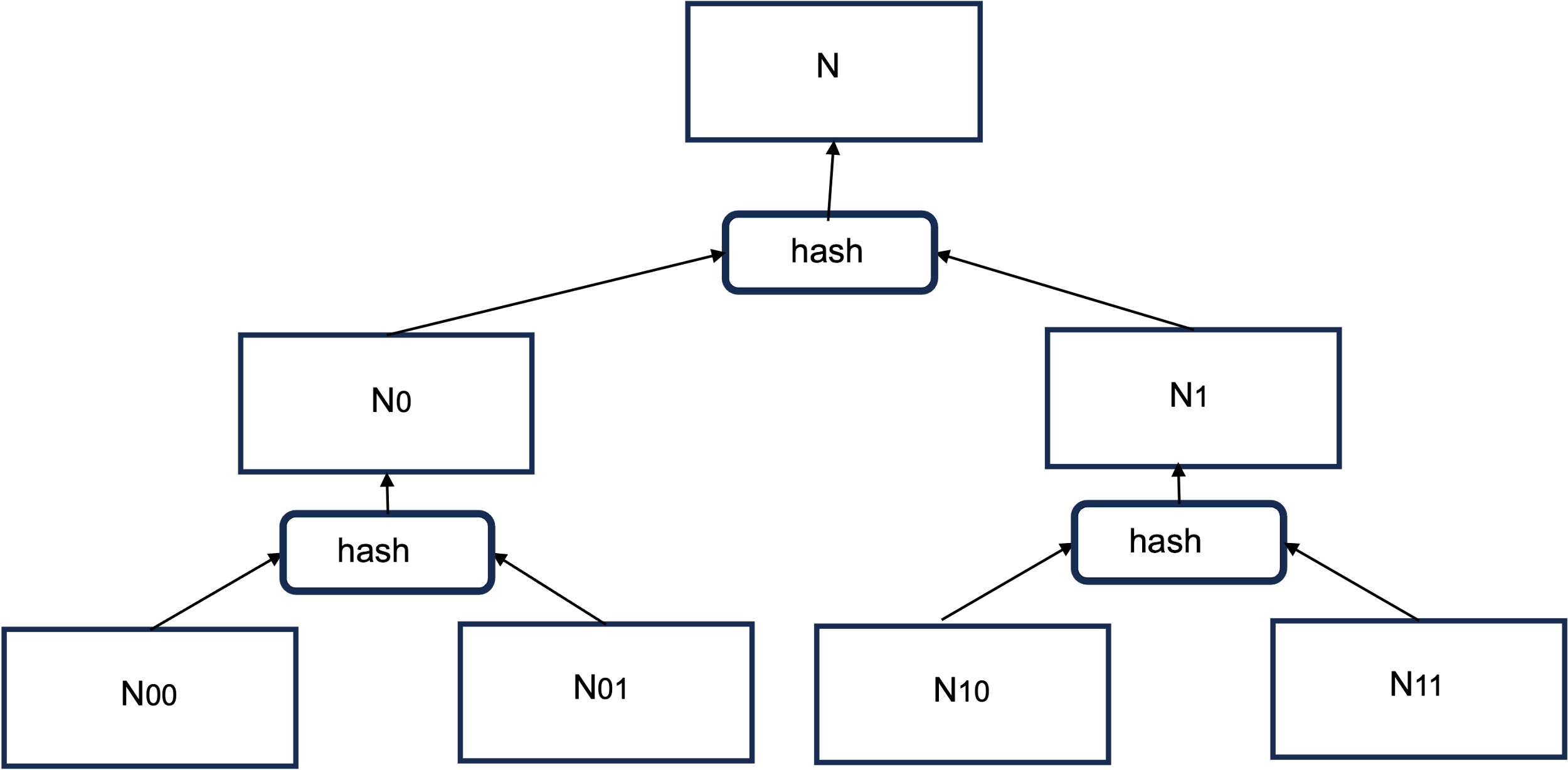
図4: 階層型ハッシュ(Merkle Tree)

一回の署名には、このツリーの中の一つのリーフから出発し、ルートノードに到達する一つのパスを使用します。一回署名に使ったパスは再度使用することはできません。端から順にリーフノードを使用するようにパスを選択すれば、使用済みのパスをインデックスとして抑えておくことができます。これが階層型ハッシュにおける状態で、署名者は二度同じ鍵を使わないように管理します。

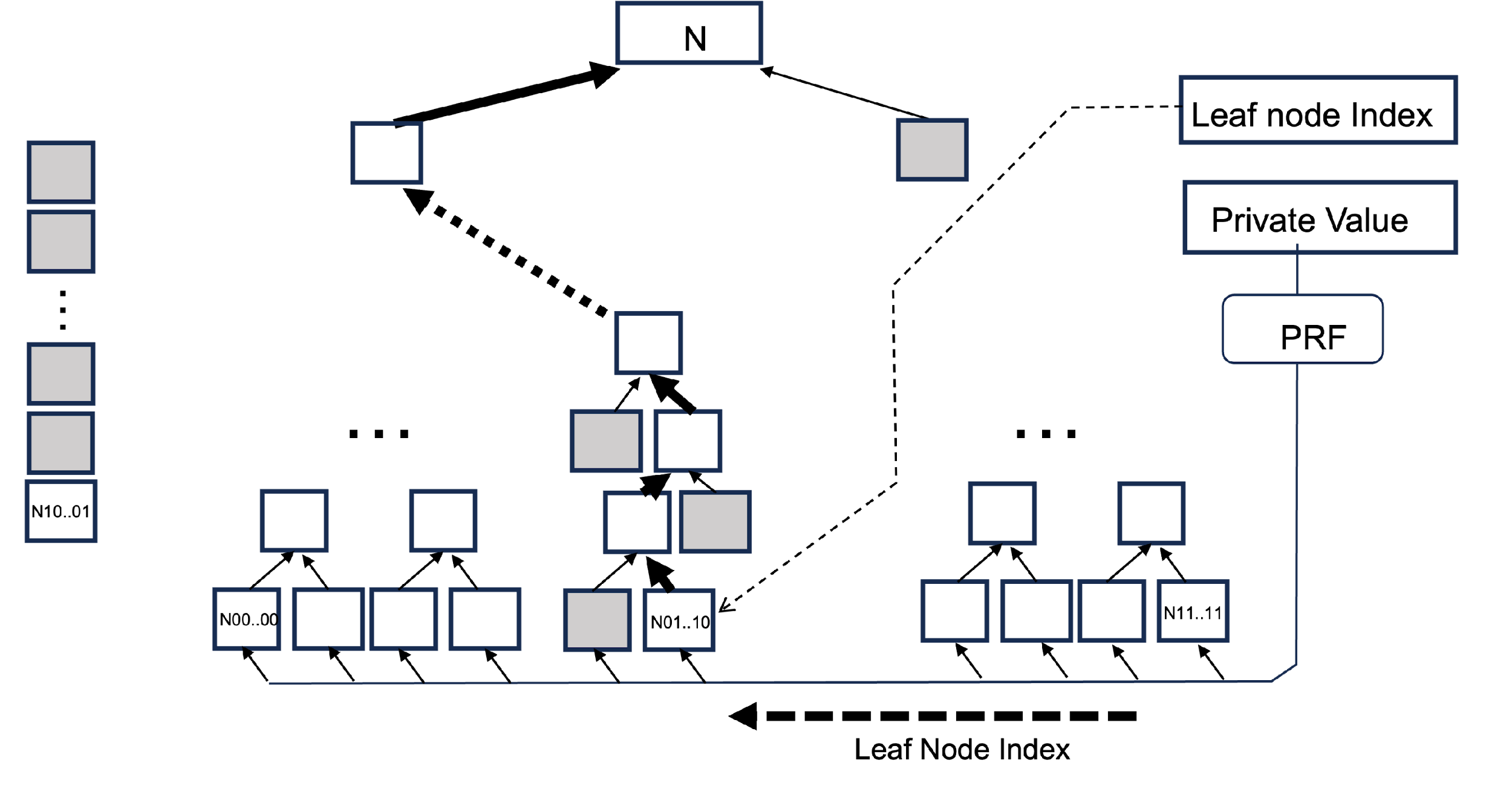
図5: リーフノードのインデックス

この方式の署名は利用に若干の注意が必要です。ワンタイム署名ですので、使用した署名を再び使わないように状態を管理する必要があります。また、生成できる署名の数はリーフノードの数で制限されます。そのため、セキュアプロトコルのように非常に多数の署名を生成しなければならない場合、数の上限を決めることが難しいような用途には向きません。また、その数は署名の長さとのトレードオフになるので用途によって適当な調整が必要となります。

階層型ハッシュにはそのような留意点がある一方で、ベースとなるアルゴリズムは従来から長年の利用実績のあるハッシュ関数の一方向性のみを利用しています。そのため、今のところ量子コンピューティングによる脅威について比較的予測可能とされている点が最大の強みかと思います。また、格子ベースのML-DSAに比べると署名サイズを短くできるので、IoTデバイスのような小型のもののセキュアブートなどの用途に向いているともいえます。

アルゴリズムの標準化

さて、原理の話はこのくらいにして、それらを使ったアルゴリズムの標準化について少しまとめておきたいと思います。

先ほどから、NISTのPQCコンペティションの話を中心に紹介してきていますが、このコンペティションの結果を受けて、ご覧のように鍵のカプセル化とデジタル署名についてアルゴリズムの標準が2024年に発表されています。ML-KEMとML-DSAは格子暗号ベースのアルゴリズムであり、SLH-DSAは階層型ハッシュをベースとしたアルゴリズムに分類されます。

一方、インターネットの標準化団体であるIETFでも早い段階から量子コンピューティングの脅威についての認識が高まり、NISTより一足先に標準が発行されています。こちらは、階層型ハッシュをベースとしたデジタル署名のアルゴリズムで、

XMSS (eXtended Merkle Signature Scheme)
LMS(Leighton-Micali Signature)

の二つがあります。XMSSはより強固なセキュリティを実現できる一方で、LMSはより容易に利用できます。

以下にこれらのPQCアルゴリズムの標準についてまとめます。

IETF RFCによる標準

階層型ハッシュによるデジタル署名
RFC-8391 (NIST SP 800-208): XMSS/MT
RFC-8554 (NIST SP 800-208): LMS/HSS

NISTによる標準

鍵カプセル化
FIPS-203: ML-KEM(CRYSTALS-Kyber)
デジタル署名
FIPS-204: ML-DSA(CRYSTALS-Dilithium)
FIPS-205: SLH-DSA(SPHINCS+)

一方、米国連邦政府のCNSA2.0では、現時点では表のような、アルゴリズムとセキュリティ強度のものを推奨しています。ご覧のように、対称鍵やハッシュでは鍵長とハッシュ長の強化で対応し、鍵交換やデジタル署名では格子ベースや階層型ハッシュベースのような新しいアルゴリズム、スキームで対応します。

種別	暗号アルゴリズム	脅威への対策
対称鍵暗号	AES-256	鍵長、ハッシュ長の強化
ハッシュ	SHA-384/SHA-512	鍵長、ハッシュ長の強化
非対称鍵暗号　鍵交換　デジタル署名	ML-KEM 1024 ML-DSA-87 LMS (SHA-256/192) XMSS	新しいアルゴリズム(格子、階層型ハッシュ)

表4: CNSA2.0の推奨アルゴリズム

PQCアルゴリズムはこのように基本的なアルゴリズムとしての標準は定義されていますが、注意しなければならない点があります。PQCアルゴリズムは従来型の攻撃に十分強いとは限らないという点です。特に、格子暗号などPQCのために新たに研究されたアルゴリズムでまだ利用実績の短いものは、たとえ厳しいコンペティションに勝ち抜いたものと言えども絶対的な保証があるわけではありません。そのためNISTでは従来型アルゴリズムとのハイブリッド化をした上での利用を推奨しています。

IETFでは具体的なハイブリッドの組み合わせに関する議論が進んでいて、正式なRFC発行には至っていませんが(2025年3月時点)、TLS1.3の鍵合意に関するPQC対応のドラフト版では次のようなML-KEMと従来型の楕円曲線とのハイブリッドが定義されています。

secp256r1 ECDH with ML-KEM-768
X25519 ECDH with ML-KEM-768
secp384r1 ECDH with ML-KEM-1024

アルゴリズムの実際

次に、アルゴリズムの実際について見ていくことにします。

wolfSSL v5.7.6では、これまで見てきた標準に準拠した独自開発のPQCアルゴリズムの実装を製品化しています。これらのアルゴリズムはwolfSSLの商用ライセンス版と共に無償オープンソース版にも含まれており、技術評価することができます。ここではそのwolfSSL v5.7.6のPQCについて実際の内容を見ていきます。

PQCでまず注意しなければいけないのは鍵サイズかと思います。図6の棒グラフは鍵サイズを従来型暗号と比較しています。従来型暗号のRSAや楕円曲線のECDHなどに比べて、多くの場合実用の範囲であると思いますが、非常に大きくなることがわかります。

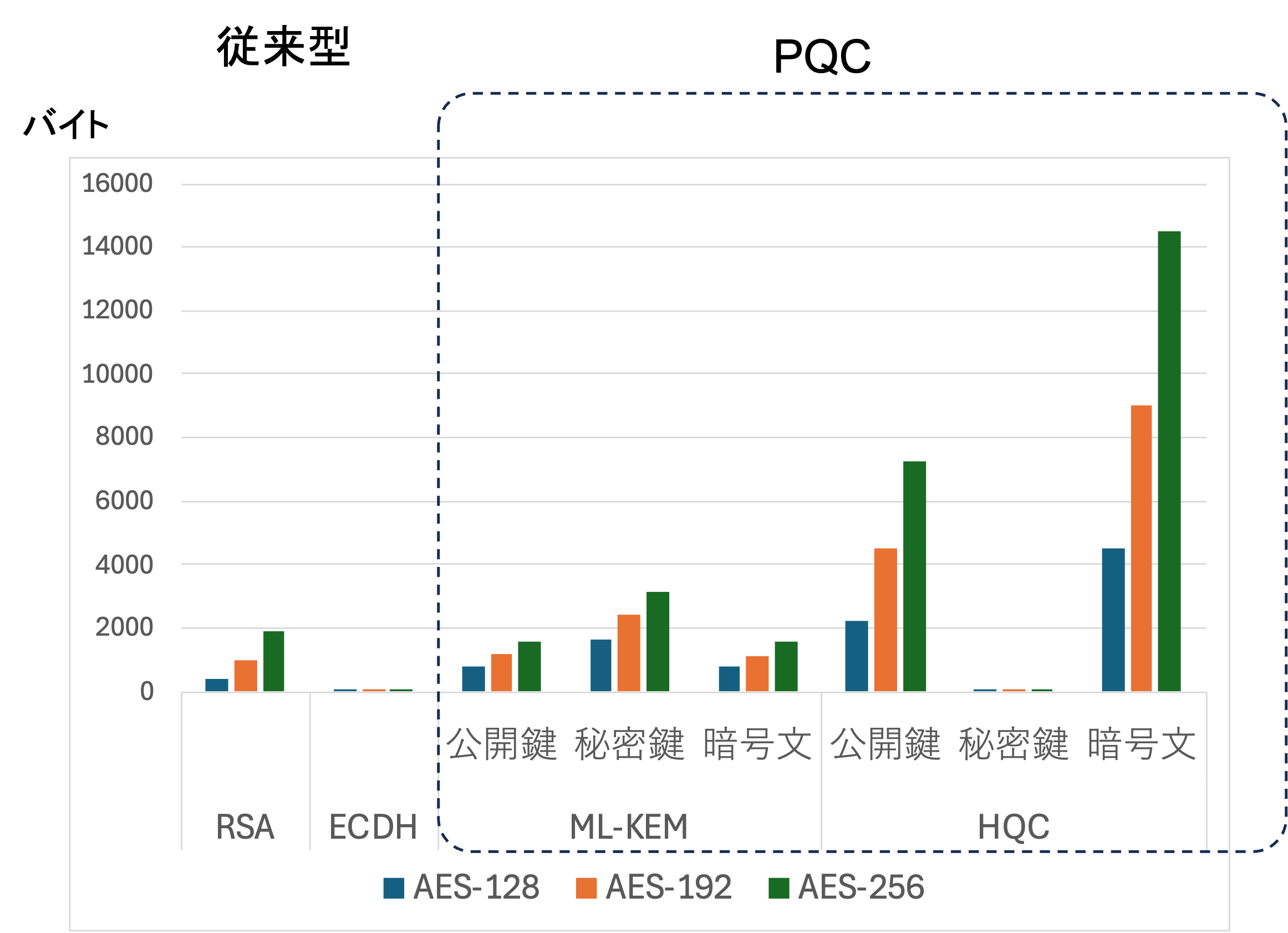
図6: 鍵サイズの比較 (ML-KEM, HQC)

同じ図6では、鍵サイズと合わせて暗号文のサイズも示しています。KEMによる鍵交換の場合、図7のように暗号化された共有値も通信相手にメッセージとして送られるので、そのサイズも考慮する必要があります。従来型のアルゴリズムでは、暗号文のサイズは元のメッセージサイズとほぼ同じとなりますが、PQCの場合、HQCのように暗号文のサイズは元のメッセージのサイズにかかわらず大きく膨らむものもあります。

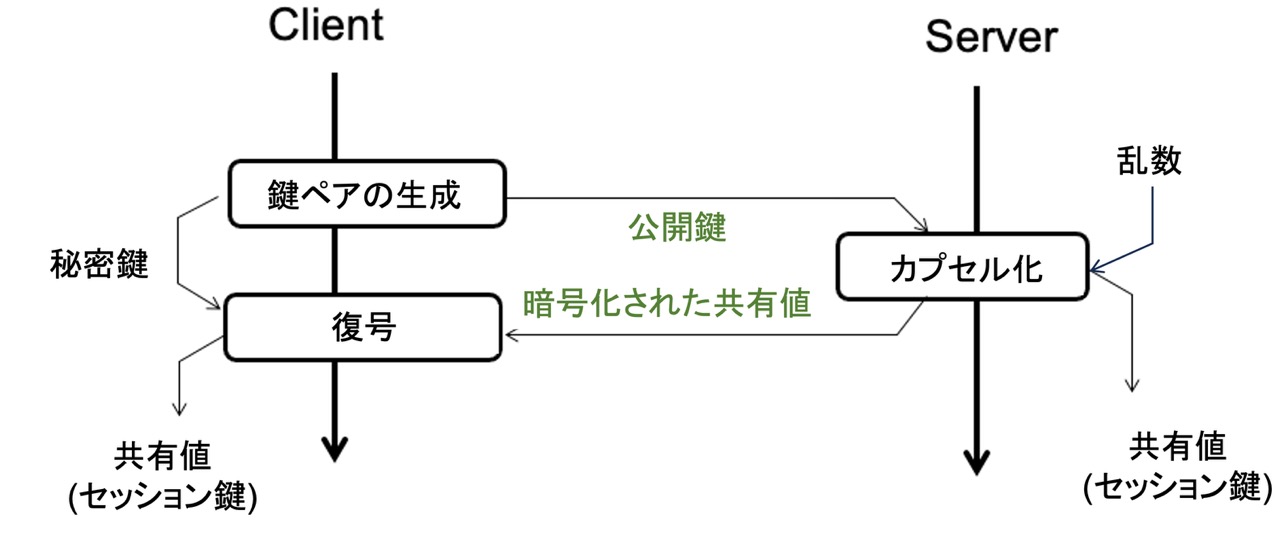
図7: KEMモデルによる鍵交換

PQCアルゴリズムの処理性能ですが、図8のグラフは従来型のECDHとML-KEMによるカプセル化と復号の所要時間を相対的に比較したものです。縦軸は所要時間を表すので、長いほうが遅いことを意味しています。ベンチマークには弊社のwolfSSL v5.7.6に含まれるwolfCryptを使用しています。

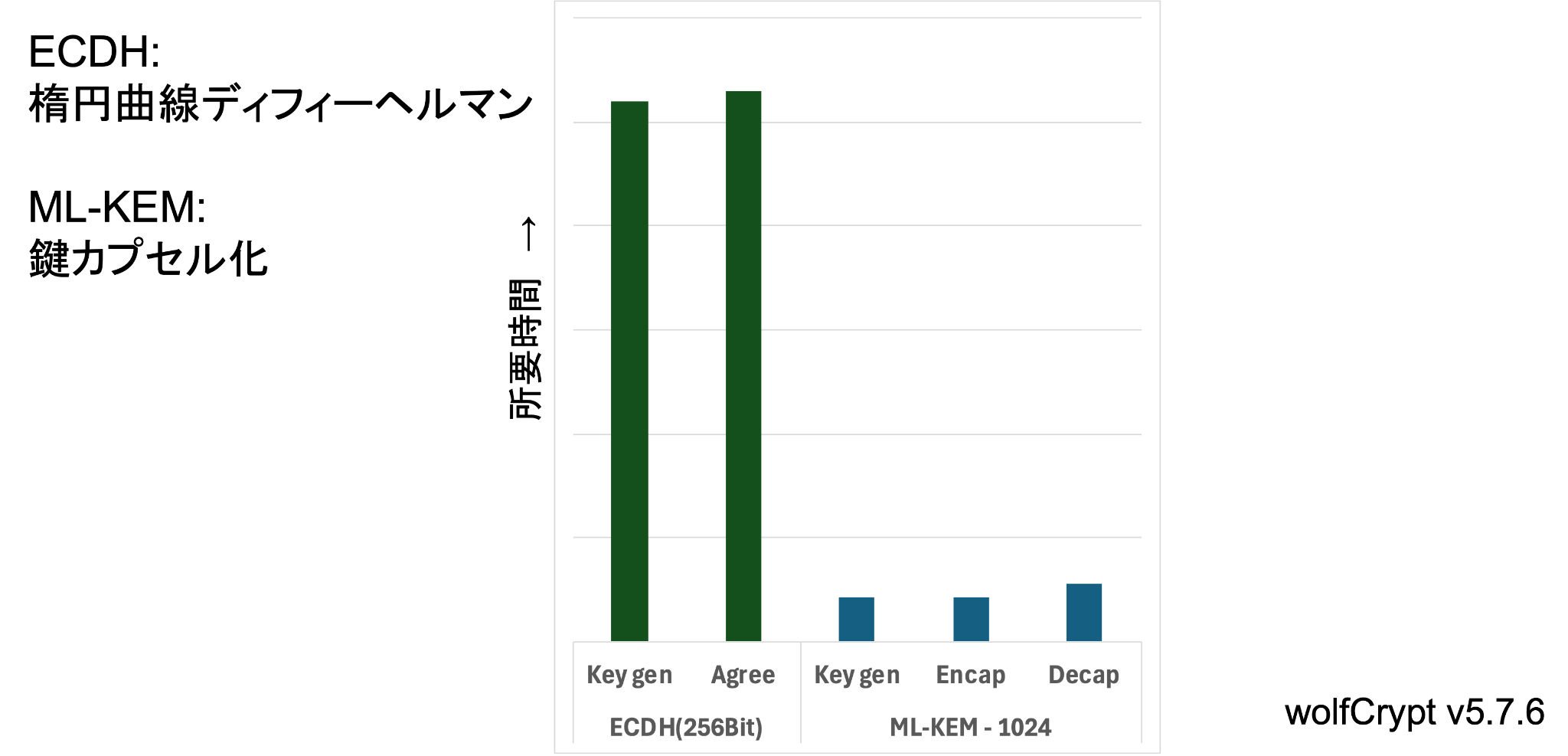
図8: 従来型とPQCの性能比較 (鍵交換)

直感的にはPQCのアルゴリズムの方が量子コンピュータの高い演算能力に対抗するために所要時間も余計にかかるように思われるかもしれませんが、実際には、格子ベースのアルゴリズムの方が却って短い所要時間となっています。

さらにECDHの場合、クライアント、サーバ双方で鍵生成、アグリーメントの処理が
行われるので公平な比較のためにはECDHの所要時間はこれらを二倍する必要があります。

ただし、前述したように、NISTでは、PQCのアルゴリズムと従来型アルゴリズムを組み合わせたハイブリッドアルゴリズムとして使用することを強く推奨しています。当然ながら、その場合、所要時間は従来型プラスPQCアルゴリズムの所要時間となります。

図9では、署名検証について、従来型のECDSAとPQCのML-DSAでの、鍵生成、署名、検証のそれぞれの所要時間を比較しています。こちらは、鍵カプセル化のECDHとML-KEMの差ほど顕著ではないですが、ML-DSAのほうがやや所要時間が短い傾向がみられます。

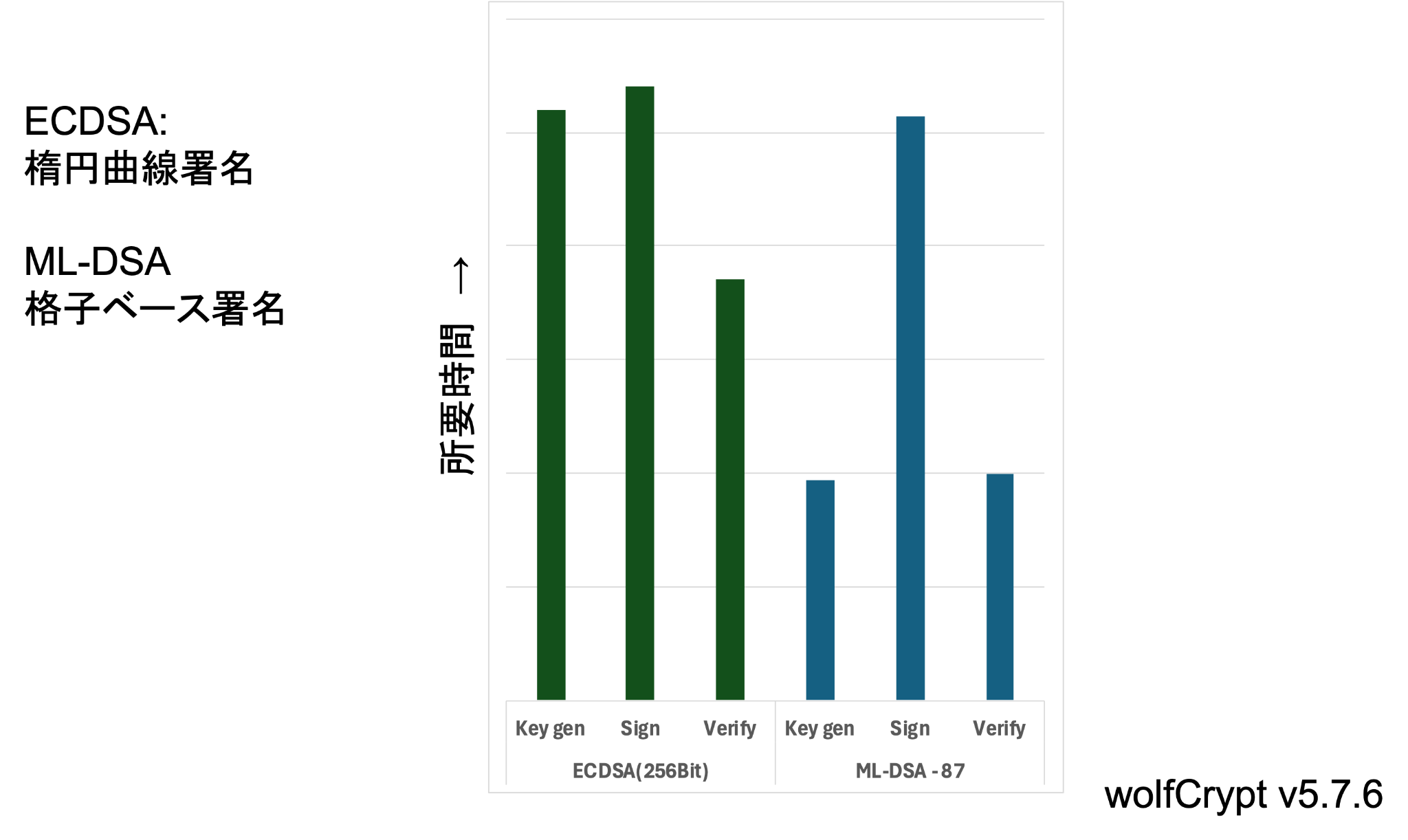
図9: 従来型とPQCの性能比較：デジタル署名 (格子暗号ベース)

図10では、XMSS、LMSのデジタル署名の署名検証を、同程度のセキュリティ強度を持つRSAと処理時間を比較してみました。従来型のRSAに比べて処理時間は長くなってしまう傾向にありますが、セキュアブートのような用途であれば署名検証の回数は少ないため十分な処理速度を実現できると言えるかと思います。

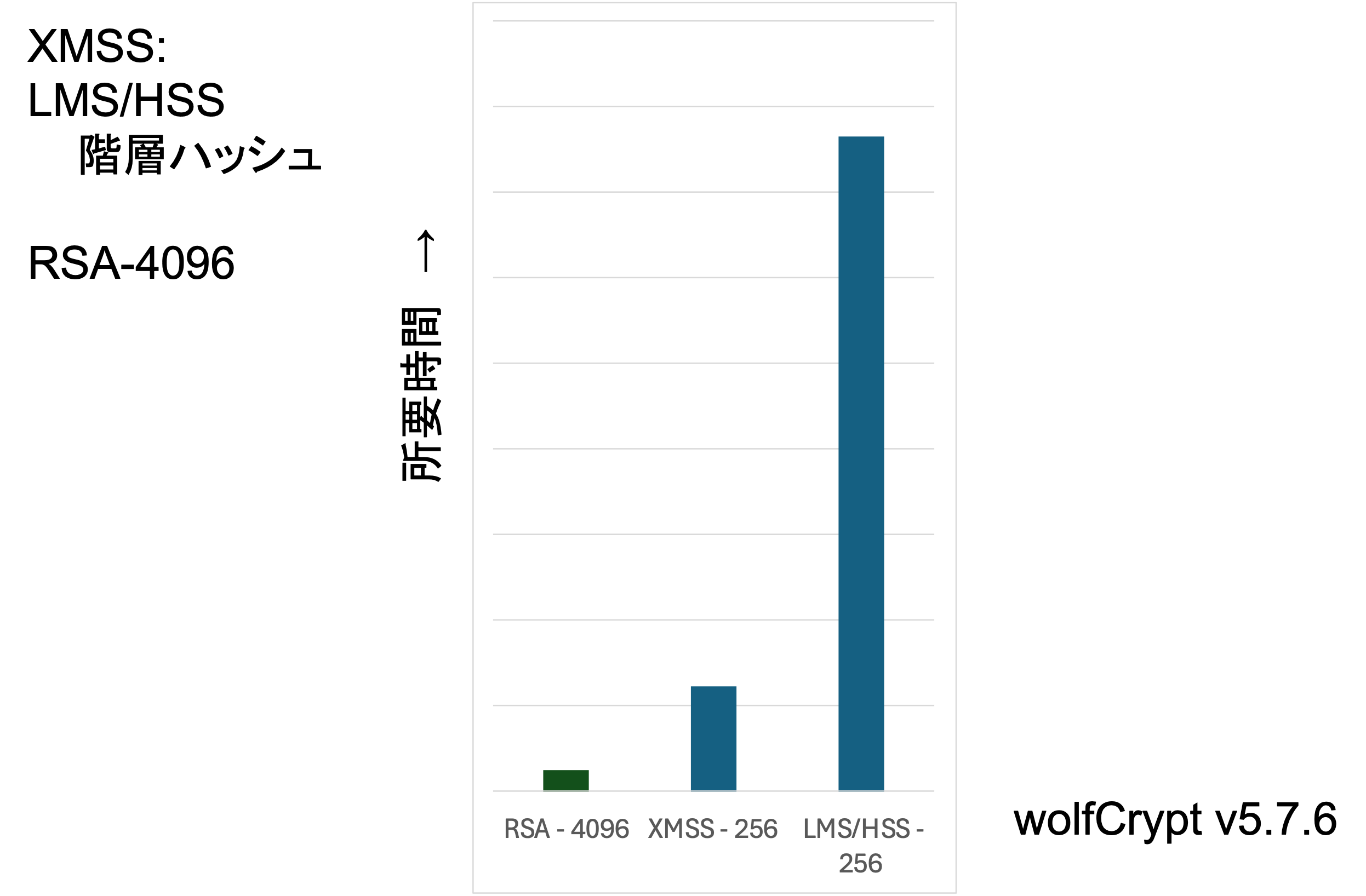
図10: 従来型とPQCの性能比較：署名検証 (階層ハッシュベース)

PQCを動作させてみる

さて、本稿の最後にこれらのPQCを実際に動作させてみることにしましょう。

wolfSSLの最新バージョンでは、これまでご紹介したNISTやIETFの標準に準拠したPQCアルゴリズムをサポートしています。PQCアルゴリズムは、無償のオープンソース版、有償商用ライセンス版の両方ともで提供しているので、技術評価の用途では無償オープンソース版をダウンロードしていただきすぐに動作させることができます。

実際のPQCアルゴリズムはwolfCrypt暗号アルゴリズムライブラリで提供されていて、wolfSSL社の各種プロトコルライブラリやブートローダ、HSM(ハードウェアセキュリティモジュール)などはwolfCryptを利用しています。

例として、wolfSSLライブラリでPQCを有効化する場合には、Githubからオープンソース版をダウンロード後、configureコマンドにオプションを指定してPQCアルゴリズムを有効化したMakefileを生成します。最後に、makeコマンドを実行しビルドします。

$ git clone --depth 1 https://github.com/wolfssl/wolfssl
$ cd wolfssl
$ ./autogen.sh
$ ./configure --enable-kyber --enable-dilithium
…
Configuration summary for wolfssl version 5.7.6
Features
   * KYBER wolfSSL impl:         yes ← 
   * DILITHIUM:                  yes ← 
…
$ make all

これで、プロトコルライブラリとともに、サンプルプログラムやベンチマークプログラムなども合わせてビルドされます。

アルゴリズムのベンチマークには、このように前のページでビルドしたベンチマークプログラムを実行します。前述の処理性能のグラフもこのコマンドで収集したデータを元にしています。

$ ./wolfcrypt/benchmark/benchmark
...
ML-KEM 1024   256  key gen     49400 ops took 1.001 sec, avg 0.020 ms, 49346.810 ops/sec
ML-KEM 1024   256    encap     47800 ops took 1.002 sec, avg 0.021 ms, 47718.972 ops/sec
ML-KEM 1024   256    decap     37300 ops took 1.002 sec, avg 0.027 ms, 37236.665 ops/sec
...
ML-DSA    87     sign      4200 ops took 1.003 sec, avg 0.239 ms, 4185.648 ops/sec
ML-DSA    87   verify      9800 ops took 1.001 sec, avg 0.102 ms, 9793.938 ops/sec
...

次に、簡単なTLSサーバとクライアントを実行させてみます。パソコン上のコマンドウィンドウで先ほどのmakeで作ったサンプルサーバをPQCオプションを指定して起動します。サンプルサーバはクライアントからのTLS接続待ちに入ります。

$ ./examples/server/server -v 4 --pqc P521_KYBER_LEVEL5

次に先程のサーバを実行したウィンドウとは別のウィンドウでサンプルクライアントを起動すると先程のサーバとTLS接続し一往復のメッセージ通信を行い、コンソールには接続情報が出力されます。その出力にP521_KYBER_LEVEL5と表示されることから、楕円曲線暗号とKyberのハイブリッドアルゴリズムで接続が成立したことがわかります。

$ ./examples/client/client -v 4 --pqc P521_KYBER_LEVEL5
Using Post-Quantum KEM: P521_KYBER_LEVEL5
Alternate cert chain used
 issuer : /C=US/ST=Montana/L=Bozeman/O=Sawtooth/OU=Consulting/CN=www.wolfssl.com/emailAddress=info@wolfssl.com
 subject: /C=US/ST=Montana/L=Bozeman/O=wolfSSL/OU=Support/CN=www.wolfssl.com/emailAddress=info@wolfssl.com
 altname = example.com
 serial number:01 
SSL version is TLSv1.3
SSL cipher suite is TLS_AES_128_GCM_SHA256
SSL signature algorithm is (null)
SSL curve name is SECP521R1
Session timeout set to 500 seconds
Client Random : 218C741111D307A2841373F8872AE8F45F1D06EB7E7064F38D5FBFFEC6345B5E
I hear you fa shizzle!

同時に、サーバ側のウィンドウにはサーバの接続情報がクライアントのウィンドウと同様に表示されます。こちらでも、P521_KYBER_LEVEL5のPQCが使われたことが表示されます。

$ ./examples/server/server -v 4 --pqc P521_KYBER_LEVEL5
Using Post-Quantum KEM: P521_KYBER_LEVEL5
Alternate cert chain used
 issuer : /C=US/ST=Montana/L=Bozeman/O=wolfSSL_2048/OU=Programming-2048/CN=www.wolfssl.com/emailAddress=info@wolfssl.com
 subject: /C=US/ST=Montana/L=Bozeman/O=wolfSSL_2048/OU=Programming-2048/CN=www.wolfssl.com/emailAddress=info@wolfssl.com
 altname = example.com
 serial number:53:16:7c:a0:56:50:46:27:82:ed:60:b4:da:33:d8:6a:c0:ea:dc:31 
SSL version is TLSv1.3
SSL cipher suite is TLS_AES_128_GCM_SHA256
SSL signature algorithm is (null)
SSL curve name is SECP521R1
Server Random : A840F6090DBD557AB550F853EAC1BC88D810598299F1BED1F0ECCB96E8C9FE68
Client message: hello wolfssl!

この通信内容はWiresharkのようなパケットキャプチャーツールでモニターすることができます。TLS1.3による通信なので、最初のClientHelloとServerHelloの後は暗号化されていて内容をみることができませんが、Client HelloのSupported GroupにはKyberと楕円曲線とKyberのハイブリッドがサポートされていることがわかります。

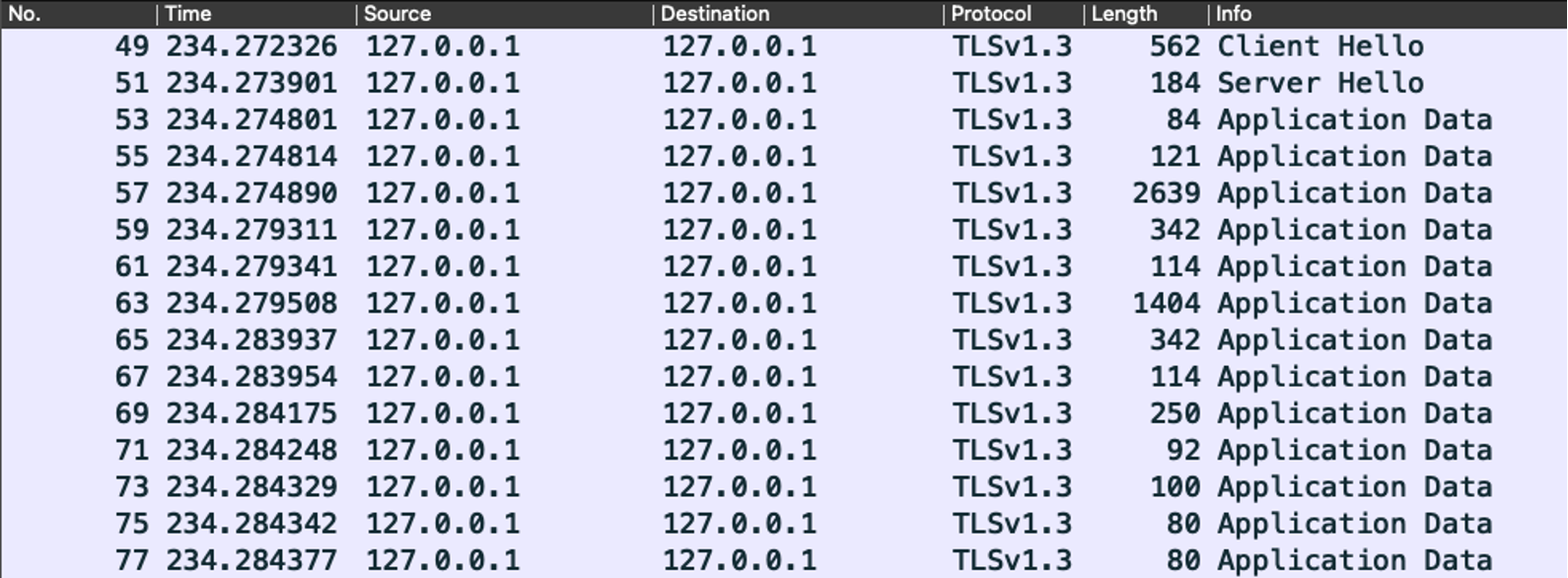
図11: TLS1.3による通信

図12: Client Hello

また、ServerHelloの内容を見ると、その中でp521_kyber1024(Level5)で接続していることがわかります。

図13: ServerHello

wolfSSLの各製品は、定期リリースのStableバージョンと最新バージョンをそれぞれご覧のサイトからダウンロードすることができます。また、PQCに関するサンプルプログラムは本稿でご覧にいれたもの以外にも参照することができます。

定期リリース(Stable)バージョン(GPLv2)>br>商用製品版と同じ内容の無償評価用オープンソースバージョン
wolfssl.jp/download
最新バージョン(GPLv2)
www.github.com/wolfssl/wolfssl
サンプルプログラム
- サンプルサーバ、クライアント：<製品ソース>/examples/{server,client}
- ML-DSA署名・検証： github.com/wolfSSL/wolfssl-examples/tree/master/pq/ml_dsa
- X9.146証明書： github.com/wolfSSL/wolfssl-examples/tree/master/X9.146

まとめ

本稿では、PQC、耐量子暗号について、そのアルゴリズムの原理から実際まで説明してきました。また、その内容はwolfSSLの製品でもご評価いただくことができることをご紹介しました。

PQCは、一応の標準化にこぎつけ、こうして製品としての提供も開始したとはいえ、まだまだ技術の成熟度を高める過程にあります。wolfSSLはこれからも技術の進化とお客様のニーズをみつめながら常により良い製品をご提供していきます。

#セキュリティ #組み込みソフトウェア

投稿者

APS

毎月約50,000人のエンジニアが利用する「APS-WEB」の運営、エンジニア限定セミナー「APS SUMMIT」の主催、最新事例をまとめた「APSマガジン」の発行、広い知識と高い技術力を習得できる「APSワークショップ」の開催など、半導体専門技術コンテンツ・メディアとして日々新しい技術ノウハウを発信しています。